字节系a_bogus最新版本插桩分析及还原
国庆前抖音罗盘a_bogus突然更到了1.0.1.15版本，拿去年的短ab跑间歇性给数据，当时由于短ab断断续续的还能跑，假期在即就没管它了，昨天突然就g了，只能被迫开干。
由于只做商家后台不做dy前台，所以中间的长ab版本都没跟过，从星球找了一份1.0.1.5的纯算，对照着开始改。
插桩简单看了下后，发现和1.0.1.5整体流程貌似区别不大，而且整个流程日志只有四万多行，没必要费劲反编译，直接在1.0.1.5的基础上开改。
初始化时间和加密数组
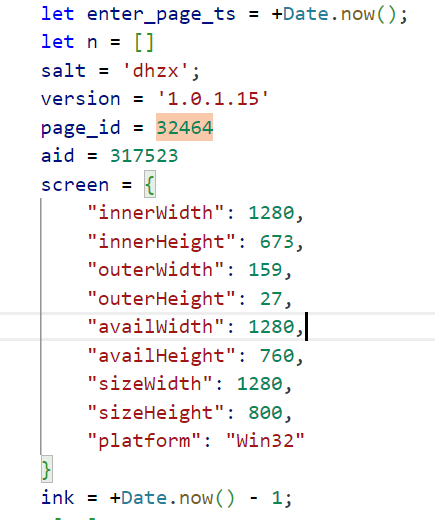
url参数处理
这里算法从短ab到1.5长ab再到1.15都没改，加盐sm3哈希，变的只有salt
请求body处理
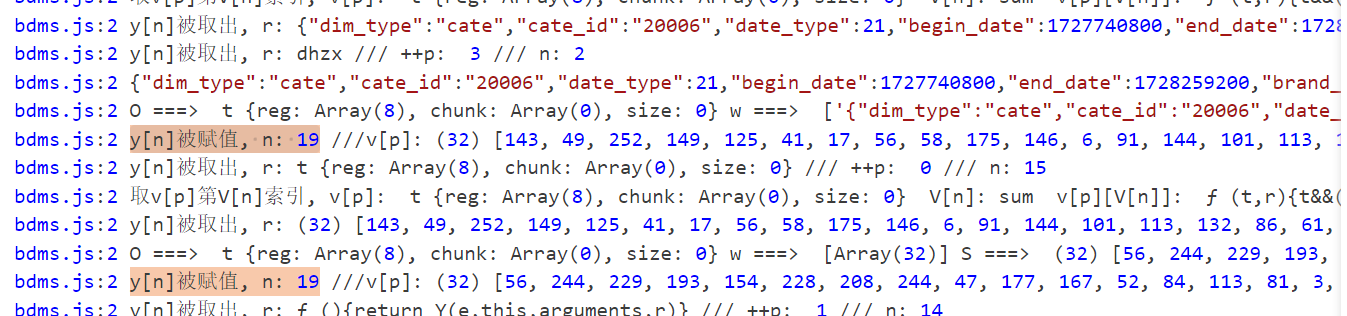
同样的加盐哈希，get方法的话就是空字符串加盐哈希
ua处理
短ab和1.5都是标准RC4，但是1.15可以明显看到进行了魔改：
S数组变成了255 254 ... 0
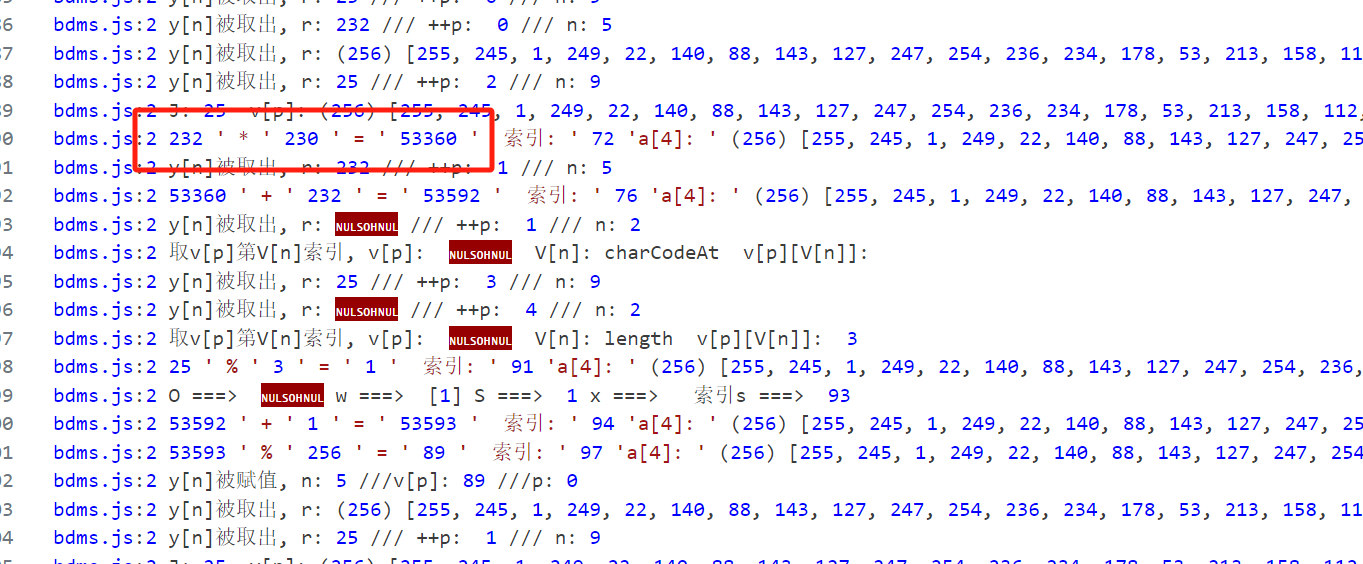
往下看，密钥生成部分出现了乘法，明显进行了魔改，不过逻辑很清晰：
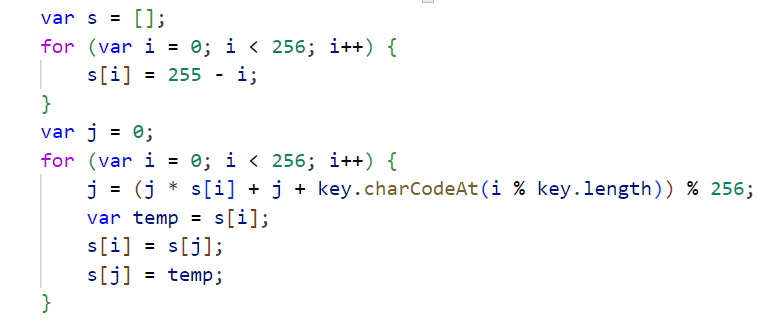
加密部分还是RC4的原生xor，实际上各种加密算法的魔改基本都是在密钥轮进行的，很少有魔改加密轮的，因为没能力/不安全。
RC4之后的魔改base64还是和之前一样，没改变：
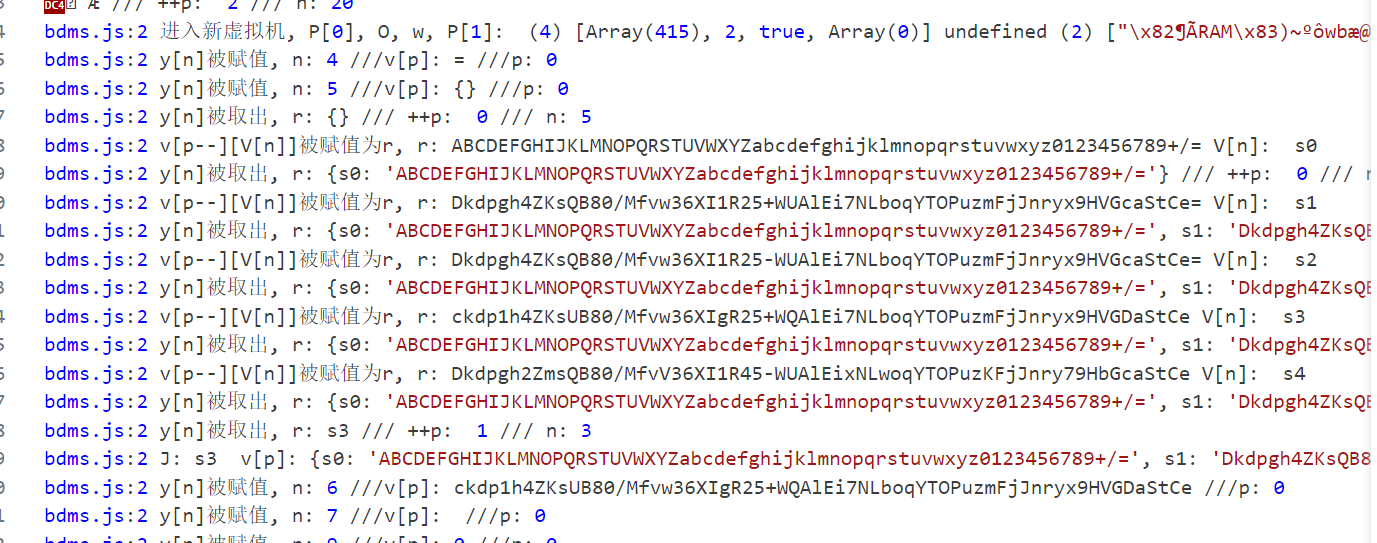
后续又是一次sm3
版本号处理
直接split后数字化。
短数组生成
对着日志撸，逻辑很清晰
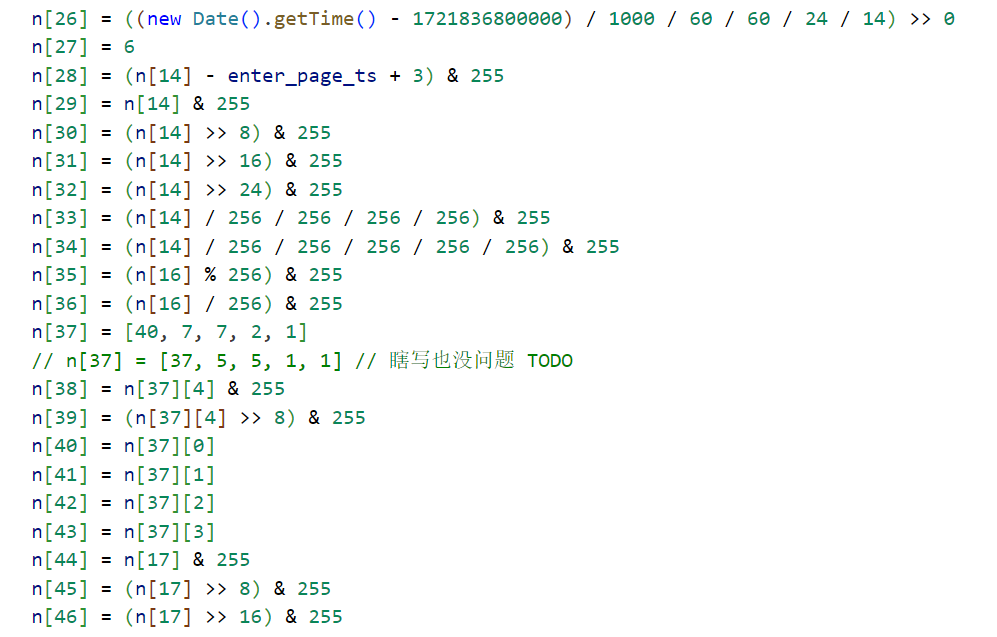
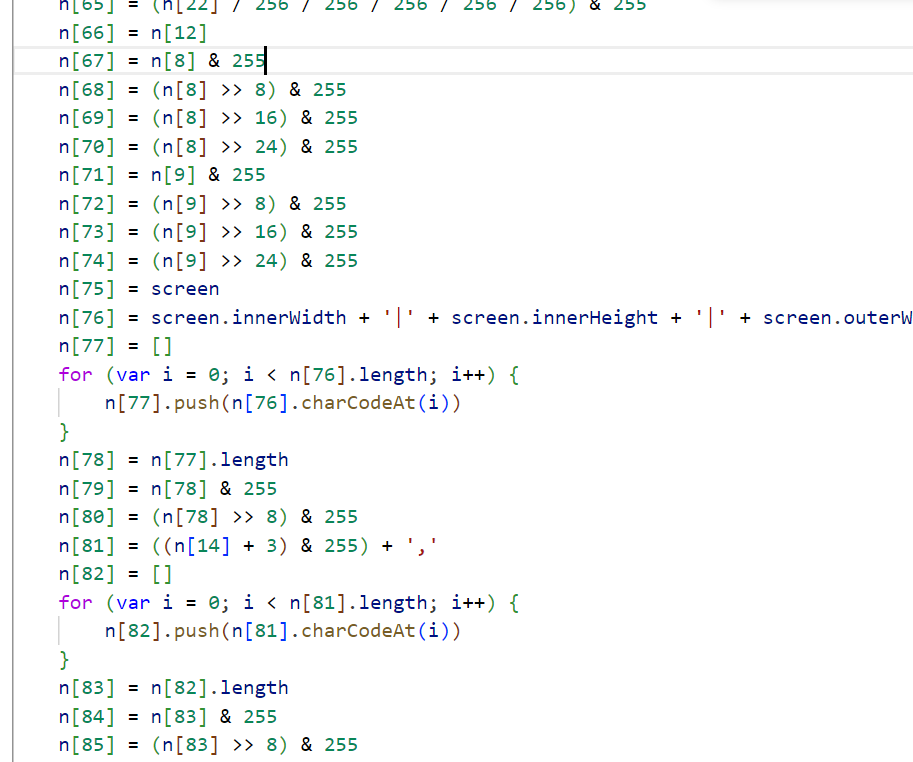
随机数生成算法
这一部分短ab没有，直接复制大佬的1.5算法。
两个位置用到，分别是：
n[86] = gener_random(Math.random() * 65535, [n[25][0], n[25][1]]).concat(gener_random(Math.random() * 65535, [n[25][2], n[25][3]]))和
n[89] = gener_random(Math.random() * 65535, [3, 82])传参其实并不都是Math.random() * 65535，但是能用就懒得改。
短数组转长数组
n[87] = n[86][0] ^ n[86][1] ^ n[86][2] ^ n[86][3] ^ n[86][4] ^ n[86][5] ^ n[86][6] ^ n[86][7] ^ n[24] ^ n[26] ^ n[27] ^ n[28] ^ n[29] ^ n[30] ^ n[31] ^ n[32] ^ n[33] ^ n[34] ^ n[35] ^ n[36] ^ n[38] ^ n[39] ^ n[40] ^ n[41] ^ n[42] ^ n[43] ^ n[44] ^ n[45] ^ n[46] ^ n[47] ^ n[48] ^ n[49] ^ n[51] ^ n[52] ^ n[53] ^ n[55] ^ n[56] ^ n[57] ^ n[59] ^ n[60] ^ n[61] ^ n[62] ^ n[63] ^ n[64] ^ n[65] ^ n[66] ^ n[67] ^ n[68] ^ n[69] ^ n[70] ^ n[71] ^ n[72] ^ n[73] ^ n[74] ^ n[79] ^ n[80] ^ n[84] ^ n[85]
new_list = [n[34], n[44], n[56], n[61], n[73], n[29], n[70], n[45], n[35], n[49], n[38], n[66], n[51], n[68], n[28], n[48], n[64], n[47], n[30], n[71], n[26], n[55], n[31], n[69], n[59], n[40], n[62], n[63], n[27], n[72], n[41], n[74], n[57], n[52], n[42], n[39], n[33], n[67], n[53], n[43], n[65], n[46], n[36], n[24], n[60], n[32], n[79], n[80], n[84], n[85]]
n[88] = new_list.concat(n[77], n[82], [n[87]])先是xor生成校验位，然后拼接生成短数组n[88]。
接着一顿操作把94位数组变成了125位数组。
这里询问一个搞完的大佬几个数字是否是常量，结果大佬直接把这部分代码发我了= =
function arr94_to_arr125(arr94) {
let result = [];
let number_of_loops = 0;
const xor_array = [145, 110, 66, 189, 44, 211];
number_of_loops = Math.floor(arr94.length / 3);
for (let i = 0, j = 0; i < number_of_loops; i++) {
j = i * 3;
let y = (Math.random() * 1000) & 255;
result.push(y & xor_array[0] | (arr94[j] & xor_array[1]));
result.push(y & xor_array[2] | (arr94[j + 1] & xor_array[3]));
result.push(y & xor_array[4] | (arr94[j + 2] & xor_array[5]));
result.push((arr94[j] & xor_array[0]) | (arr94[j + 1] & xor_array[2]) | arr94[j + 2] & xor_array[4]);
}
result.push(arr94[93]);
return result;
}
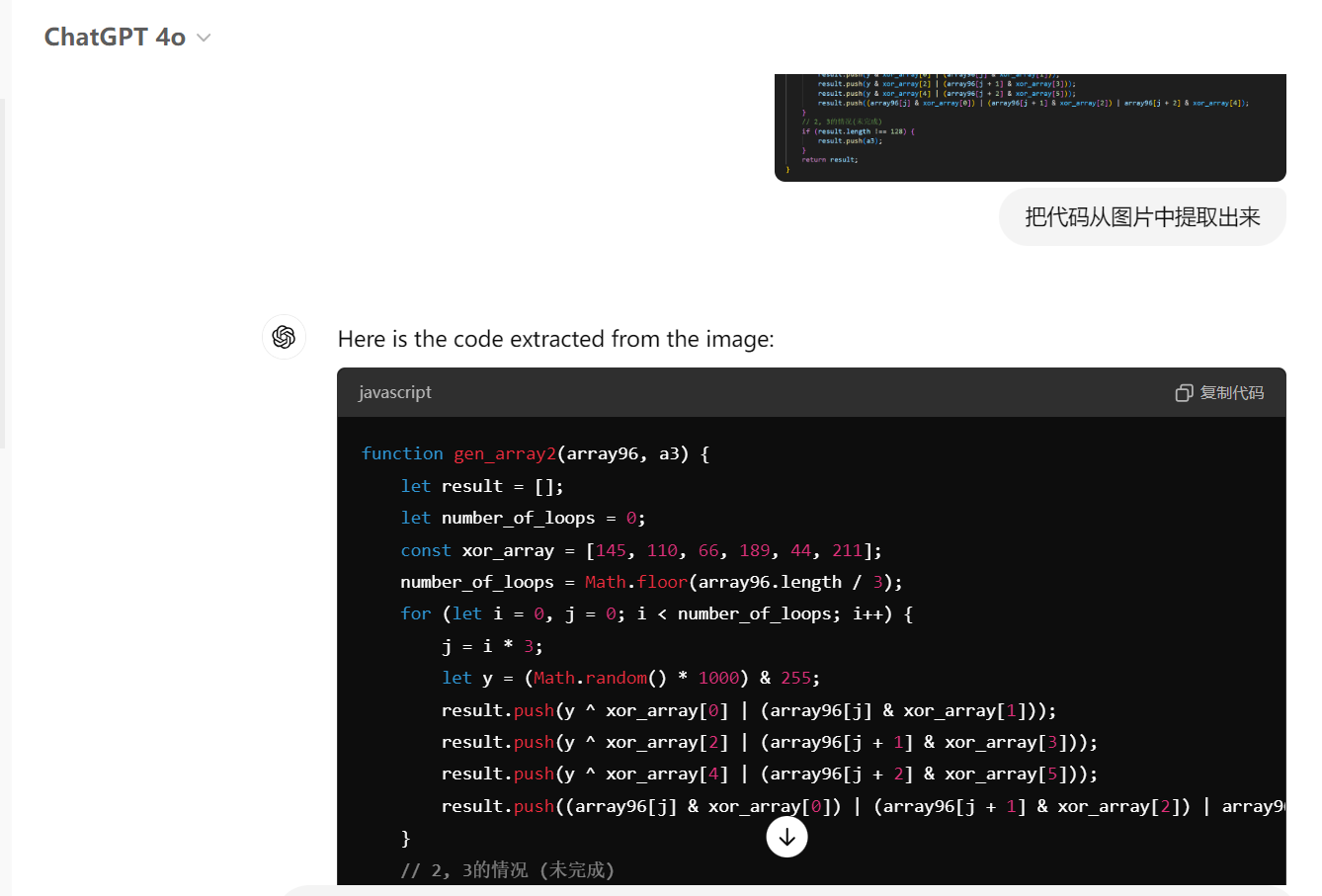
不过大佬发的是1.0.1.17版本抖音短视频的sdk，我改了下后发现死活过不去，还以为是1.17在1.15基础上又变了，最后调试后发现原来是弱智GPT提取代码时搞错了几个运算符，GPT给我拉了一坨大的......
生成ab
版本号数组拼接上面的125数组后RC4，然后另外两个常量生成的字符串再拼接，最后同样的魔改B64，得到的a[93]就是最终ab。
经测试1.0.1.15可以通过dy 1.0.1.17的签名认证。
扩展
上面的整个流程除了arr94_to_arr125外，其它的流程和1.5流程变化不大，硬说变化就是数组位置、加密方法的改变。
这里看到arr94_to_arr125时候就很好奇，上面的其它加密都是魔改rc4 sm3 b64的，而这个通过随机数算法加密生成的新数组，在抖音服务器那边如何解密还原呢？问了GPT，回答又是答非所问的一坨，于是问了下密码学大佬，发现这里的常量数组[145, 110, 66, 189, 44, 211]选的很有深意，因为它们的二进制为：
10010001
01101110
01000010
10111101
00101100
11010011每一组的两个都是互补的，通过位运算将加密后，完全可以通过结果的四个数字逆推得到原始数组，消除中间随机数带来的影响。
function arr125_to_arr94(arr125) {
let result = [];
const xor_array = [145, 110, 66, 189, 44, 211];
const number_of_loops = Math.floor((arr125.length - 1) / 4);
for (let i = 0; i < number_of_loops; i++) {
const r0 = arr125[i * 4];
const r1 = arr125[i * 4 + 1];
const r2 = arr125[i * 4 + 2];
const r3 = arr125[i * 4 + 3];
let x0 = 0, x1 = 0, x2 = 0;
// 逐位恢复 x0, x1, x2
for (let b = 0; b < 8; b++) {
const s0_b = (xor_array[0] >> b) & 1;
const s1_b = (xor_array[1] >> b) & 1;
const s2_b = (xor_array[2] >> b) & 1;
const s3_b = (xor_array[3] >> b) & 1;
const s4_b = (xor_array[4] >> b) & 1;
const s5_b = (xor_array[5] >> b) & 1;
const r0_b = (r0 >> b) & 1;
const r1_b = (r1 >> b) & 1;
const r2_b = (r2 >> b) & 1;
const r3_b = (r3 >> b) & 1;
let x0_b = 0, x1_b = 0, x2_b = 0;
// 根据按位操作的特性，推导 x0_b, x1_b, x2_b
if (s1_b) {
x0_b = r0_b;
} else if (s0_b) {
// 当 s1_b 为 0，s0_b 为 1 时
x0_b = r3_b;
}
if (s3_b) {
x1_b = r1_b;
} else if (s2_b) {
// 当 s3_b 为 0，s2_b 为 1 时
x1_b = r3_b;
}
if (s5_b) {
x2_b = r2_b;
} else if (s4_b) {
// 当 s5_b 为 0，s4_b 为 1 时
x2_b = r3_b;
}
// 组合比特位
x0 |= x0_b << b;
x1 |= x1_b << b;
x2 |= x2_b << b;
}
result.push(x0);
result.push(x1);
result.push(x2);
}
result.push(arr125[124]);
return result;
}神奇的密码学~