从227谈控制流平坦化的还原(一)
导言
这篇文章很久之前在知乎写的了,最近看到蔡老板ast群里有人拿九大节点合并算法+这篇文章的节点转换+自己思路通杀控制流,就搬过来了。
本打算分为三篇来写,一是节点判断和if/for的还原,二是continue/break的判断和还原,三是具体的代码实现,但是由于驱动力不足,所以二和三要到228出来时候才会写了。
三层转一层不再多说。
最后一层以switch+代码块索引的修改控制流程,其实颇为常见,初次还原起来非常头疼。
关键步骤一: 剔除控制流虚假条件。
什么叫虚假条件?某些三元表达式或者if语句的判断条件,它们为固定的几个变量名,运行到它们的时候会固定返回true或false,进入对应正确流程分支。错误分支并不是无用分支,而是随便指了一个其它节点的分支,在代码运行到这些虚假条件时候并不会进入这些位置,但是在其它分支可能会进入这个否条件分支的位置。这些虚假条件存在的最主要目的并不是产生错值或者反调试,而是为了增加反混淆的难度。
[快捷步骤二 蔡老板知识星球中的九大节点还原算法]
步骤二 理解与思考
一份代码的正常流程无非就三种: 顺序执行、判断语句及循环。而227(下文均将控制流平坦化流程称为227流程)的流程控制理解起来很简单,即改变控制流程的变量进入相应索引的代码分支。
顺序执行
改变控制变量为下一个代码分支的索引。这个不必多说,正常代码流程和227流程均为a=>b
判断语句
改变控制变量为不同布尔条件下的分支索引。
正常流程为
if(a){
b;
}else{
c;
}
d;
e;
...
227流程为
if(a){
b;
d;
e;
...
}else{
b;
d;
e;
...
}只要我们能确定a分支和d分支,就能将if语句还原。
循环语句
227的循环语句在代码形式上和判断语句差不多太多。将判断语句的判断条件作为循环的判断条件,true分支为循环体,循环体执行完毕后,又指回了判断条件再次判断。false分支则为跳出循环后的代码。
正常流程为
for(;a>b;){
c;
b++
}
d;
... 227流程为
if(a>b){
c;
b++;
goto if(a>b)
}else{
d;
...
}就是说找到(a>b)这个条件分支,就能将循环语句还原。
步骤三 想象与还原
根据上面可以知道,每块代码分支都对应着一个或者两个分支。我们可以把代码控制流的走向想象成树结构
一个标准if语句的代码及对应树结构如下:
if (a) {
b;
d;
f;
g;
} else {
c;
e;
}
h;
i;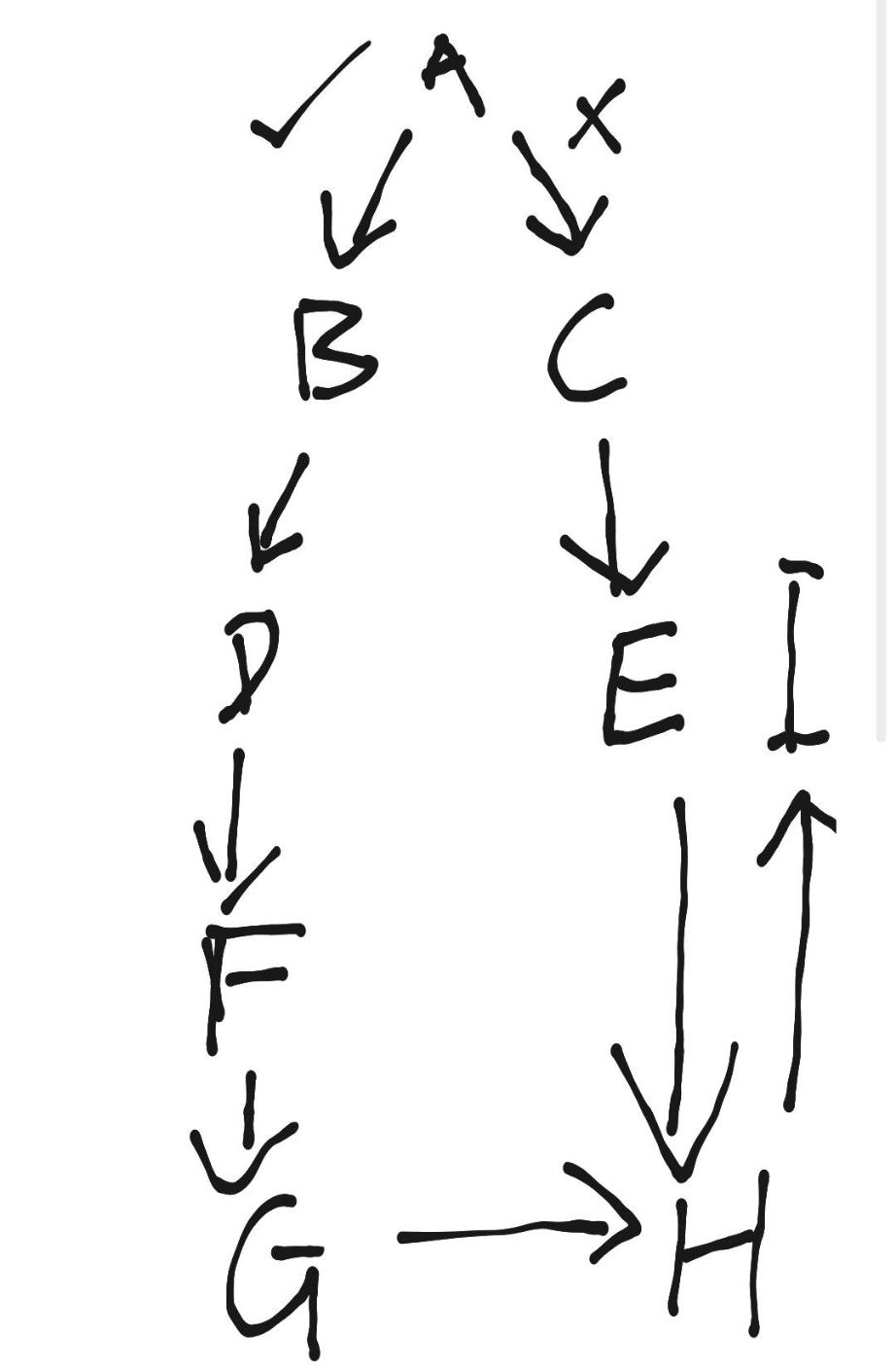
我们先明确下叫法,图中a为双向节点(两个指向),b c d等为单向节点(一个指向)。另外,当我们成功还原if语句后,if语句就从一个双向节点变成了一个单向节点(直接从a指向了h,bcdefg都被合并到了a中)。for语句也同理,还原成功后就从双向节点变成了单向节点。
上面说了,只要确定图中a和h,就能还原if语句。那么来看看怎么还原这个if语句。
当遇到双向节点的时候,我们可以肯定,它一定是if语句或者for语句的根节点。先不考虑for语句,该怎么找if语句的合并节点(图中h)呢?
一个最简单的做法,为节点a的左右两侧树枝分别设立两个空数组左=[],右=[]。然后开始遍历左右两侧节点,分别将遍历到的节点加入自己侧的数组,并在加入时判断该节点是否已经在另一侧数组存在,如果存在,那这个节点就是这个if语句的合并节点。
当某一侧遍历到双向节点double时,则进行递归,以double为根节点,为double的两侧设置空数组并遍历比较,寻找double的合并节点。对double还原成功后,双向节点double就变成了单向节点,此时便可继续进行节点a的遍历及还原。
for语句二叉树如下:
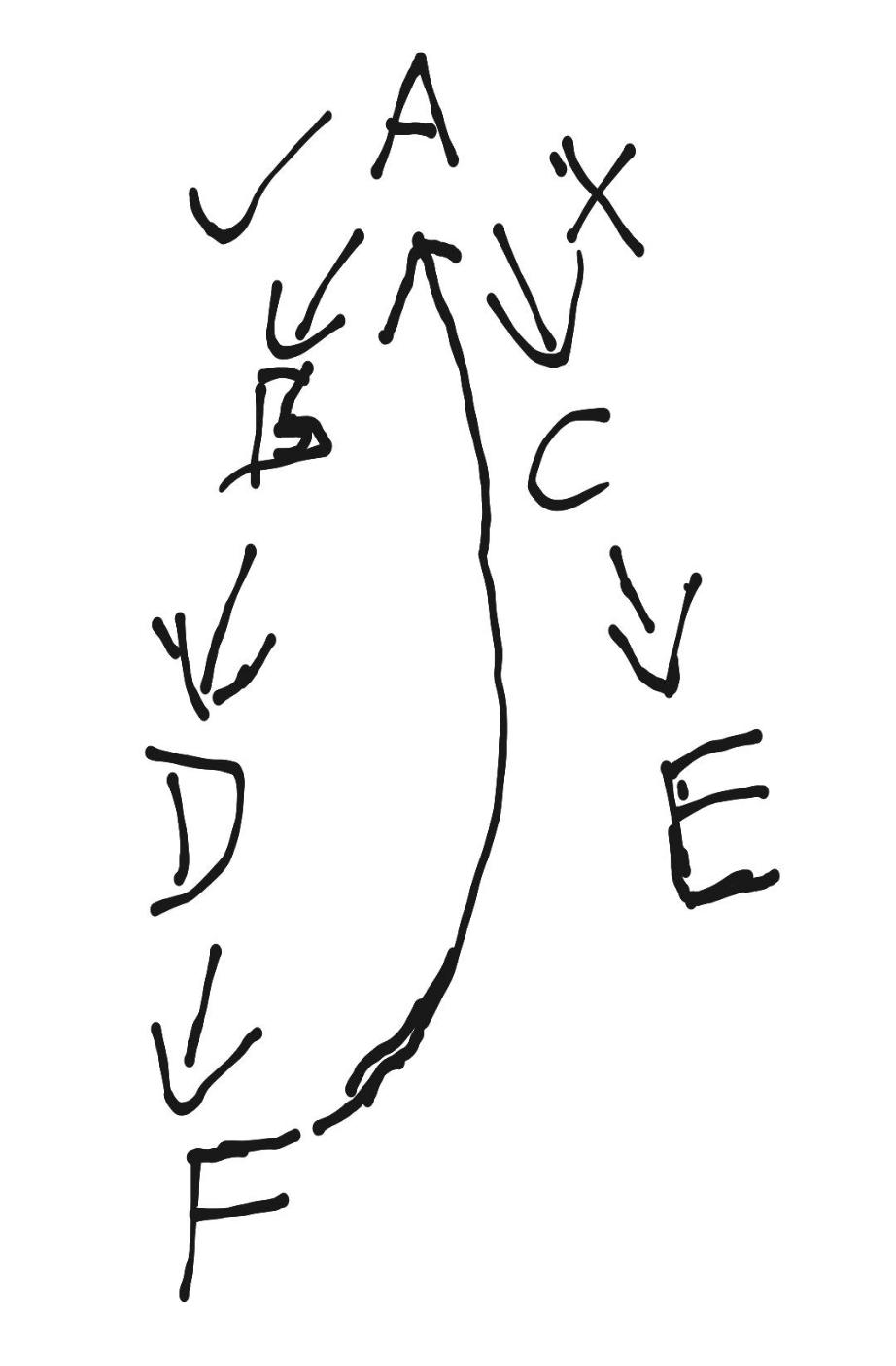
可以看到,for语句只需要确认初始节点a,就可以进行还原。
同样的,a一定是双向节点。先不考虑如何辨别a是if语句还是for循环,来看for循环的还原解法。
过程其实和if还原很相似,把a作为初始节点,接着遍历a两侧的节点,并与之与a做比较。当某侧的遍历回到a的时候,这一侧就是for循环的循环体,另一侧则是跳出循环后的语句,进而成功还原。而遍历到双向节点double的时候,同样的递归,以double为初始节点进行遍历、比较、还原,还原后双向节点double变为单向节点,此时便可继续节点a还原流程的遍历,最终成功还原a。
既然可以成功还原if和for了,下面的问题就是怎么区分一个双向节点是if语句还是for语句的初始节点呢?其实但这里就很简单了,直接为双向节点double两侧准备两个空数组,然后开始遍历并判断,如果遍历到某个节点在另一侧数组,x就是if语句,如果遍历到某个节点是double自身则为for语句,如果遍历到新的双向节点,则对新的双向节点递归还原即可。
综上,整个流程大致代码如下:
function recovery(rootNode, leftList, rightList) {
for (leftNode in leftTree){
if (leftNode.type == DoubleNode) {
replace(leftNode, recovery(leftNode, [], []))
} else {
if (leftNode == rootNode) {
return nodeToFor(rootNode, leftList, rootNode.rightTree[0])
} else {
leftList.push(leftNode)
}
}
}
for (rightNode in rightTree){
if (rightNode.type == DoubleNode) {
replace(rightNode, recovery(rightNode, [], []))
} else {
if (rightNode == rootNode) {
return nodeToFor(rootNode, rightList, rootNode.leftTree[0])
} else {
if (rightNode in leftList) {
leftIndex = leftList.indexOf(rightNode)
leftList = leftList.slice(0, leftIndex)
return nodeToIf(rootNode, leftList, rightList, rightNode)
} else {
rightList.push(rightNode)
}
}
}
}
}将case代码块根据索引和指向,递归构建一个AST树即可。文章

